🎈前言

一直都挺好奇广义线性模型（Generalized Linear Model）是怎么跑起来的。以前经常遇到这个东西，不过之前用的时候一直都在当纯粹的调包侠，没有去纠结它的原理。最近又突然想起来这个东西就在空闲时间看了一下…就…虽然和现在的前端工作也没什么关系就是了。

广义线性模型由 Nelder 和 Wed derburn 在 1972 年提出，详见 Generalized Linear Models。简单来说，广义线性模型就是使用连接函数（Link Function），使得可以是非连续、非正态的因变量可以表示为自变量的线性组合。对于线性回归模型，假设变量连续、正态。对于因变量离散、非正态的情况，线性回归模型的假设就得不到满足。而广义线性模型仅要求因变量的分布属于指数分布族（Exponential Family），对因变量没有任何的限制。

这篇博客主要是 Annette J. Dobson 的 《AN INTRODUCTION TO GENERALIZED LINEAR MODELS SECOND EDITION》的学习笔记。

🧵指数分布族

指数分布族是仅依赖一个参数 $\theta$，概率分布形式如下的分布：

$$f(y;\theta)=\exp(a(y)b(\theta)+c(\theta)+d(y))$$

当 $a(y)$ 是恒等函数时，称为自然形式（Canonical Form）：

$$f(y;\theta)=\exp(yb(\theta)+c(\theta)+d(y))$$

不难发现，正态分布、二项分布、泊松分布等很多常见的分布都属于指数分布族：

分布	密度函数	指数分布族的样子
正态	$\frac{1}{\sqrt{2 \pi}\sigma}\exp(-\frac{(y-\mu)^2}{2\sigma^2})$	$\exp(\frac{\mu}{\sigma^2}y-\frac{\mu^2}{2\sigma^2}-\frac{1}{2}\log(2\pi\sigma^2)-\frac{y^2}{2\sigma^2})$
泊松	$\frac{\lambda^k}{k!}e^{- \lambda}$	$\exp(y\log\theta - \theta-\log y!)$

分布	质量函数	指数分布族的样子
二项	$\tbinom{n}{\pi}\pi^k(1-\pi)^{n-k}$	$\exp(y \log \frac{\pi}{1-\pi}+n\log(1-\pi)+\log\tbinom{n}{y})$

假设 $Y$ 服从指数分布族，

$$\int^{+\infin}_{-\infin} f(y;\theta) \text{d}y = 1$$

如果 $f$ 和 $\frac{\partial f}{\partial \theta}$ 在 $(-\infin,+\infin) \times[m,n]$ 一致连续，

$$\frac{\text{d}}{\text{d} \theta}\int f(y;\theta) \text{d}y = \int \frac{\partial}{\partial \theta}f(y;\theta) \text{d}y = 0\\ \int f(y;\theta)(a(y)b^{\prime}(\theta)+c^{\prime}(\theta)) \text{d}y = 0$$

于是就有

$$\begin{aligned} \int f(y;\theta)a(y) \text{d}y = \text{E}(a(Y)) = -\frac{c^{\prime}(\theta)}{b^{\prime}(\theta)} &&(1) \end{aligned}$$

接下来求方差 $\text{Var}(a(Y))$，如果 $\frac{\partial^2 f}{\partial \theta^2}$ 存在，类似地，

$$\frac{\partial^2}{\partial \theta^2}f(y;\theta)=((a(y)b^{\prime\prime}(\theta))+c^{\prime\prime}(\theta))f(y;\theta)+(a(y)b^{\prime}(\theta)+c^{\prime}(\theta))^2f(y;\theta)$$

由（1）,右侧第二项可以写成

$$(b^{\prime}(\theta))^2\cdot (a(y)-\text{E}(a(Y)))^2f(y;\theta)$$

由于 $\int(a(y)-\text{E}(a(Y)))^2f(y;\theta)\text{d} y=\text{Var}(a(Y))$，$\int f(y;\theta) \text{d}y = 1$

$$\int\frac{\partial^2}{\partial \theta^2}f(y;\theta)\text{d}y=b^{\prime\prime}(\theta)\text{E}(a(Y))+c^{\prime\prime}(\theta)+(b^{\prime}(\theta))^2\text{Var}(a(Y))=0$$

于是，

$$\begin{aligned} \text{Var}(a(Y))=\frac{b^{\prime\prime}(\theta)c^{\prime}(\theta)-c^{\prime\prime}(\theta)b^{\prime}(\theta)}{(b^{\prime}(\theta))^3}&&(2) \end{aligned}$$

🧶广义线性模型

广义线性模型要求因变量 $Y_1,Y_2,\cdots Y_N$ 是独立随机变量，服从同一个自然形式的指数分布族的分布，它们的参数 $\theta_i$ 不一定相同。模型假设 $g(\text{E}(Y_i))$ 可以由 $p$（$p<N$）个自变量 $x_{ij}$ 的线性组合表示，$g$ 是连接函数：

$$\text{E}(Y_i)=\mu_i\\ g(\mu_i)=x_i^T\beta\\ x^T_i=(x_{i1},x_{i2},\cdots,x_{ip})\\ \beta=(\beta_1,\beta_,\cdots,\beta_p)^T$$

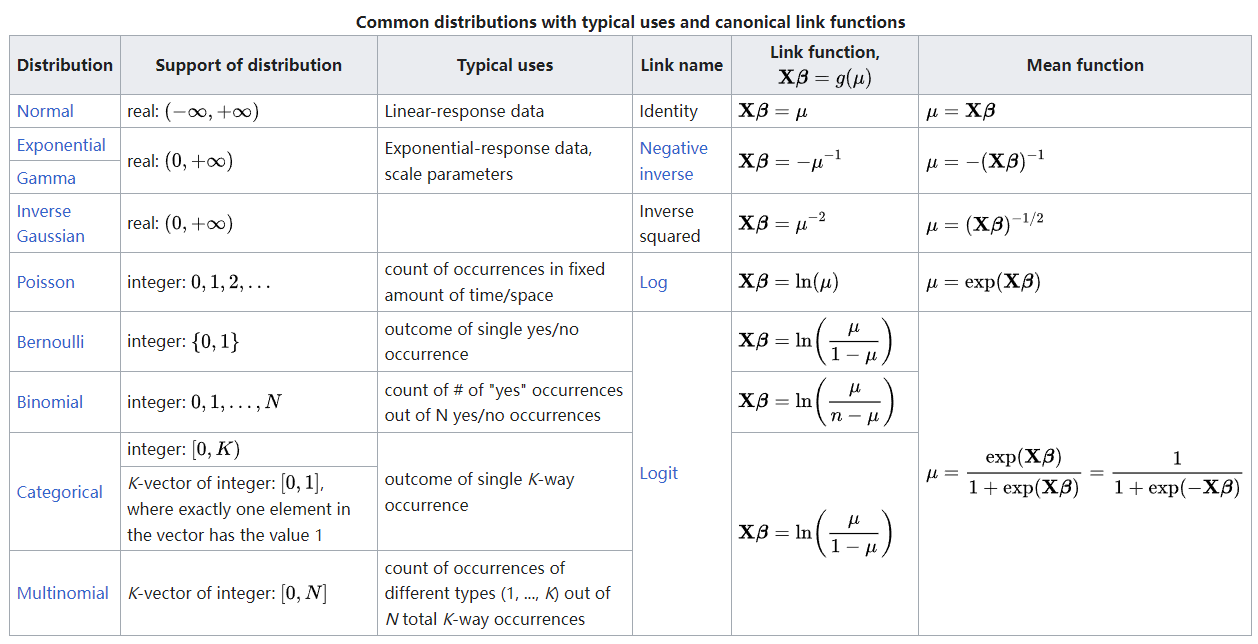
关于连接函数的选择，似乎一下子没有搜到什么资料，下面是维基百科的一个常见连接函数表格:

🔮最大似然估计

参数求解使用最大似然估计进行，对于每个 $Y_i$ 有对数似然函数：

$$l_i=y_ib(\theta_i)+c(\theta)+d(y_i)$$

加起来就是

$$l=\sum^N_{i=1}l_i=\sum y_ib(\theta_i)+\sum c(\theta) + \sum d(y_i)$$

由于难以获得解析解，这里使用牛顿法进行数值求解，迭代过程用 $b_k$ 表示 $\beta$。

$$b_{k+1}=b_k-(\nabla^2l)^{-1}\nabla l$$

$$\begin{aligned} \nabla l&_j=U_j=\frac{\partial}{\partial \beta_j}(\sum y_ib(\theta_i)+\sum c(\theta) + \sum d(y_i))\\ &=\sum_{i=1}^{N} \frac{\partial l_i}{\partial \theta_i}\frac{\partial \theta_i}{\partial \mu_i}\frac{\partial \mu_i}{\partial \beta_j} \end{aligned}\\$$

根据（1）：

$$\frac{\partial l_i}{\partial \theta_i}=y_ib^{\prime}(\theta_i)+c^{\prime}(\theta_i)=b^{\prime}(\theta_i)(y_i-\mu_i)$$

再根据（1）和（2）：

$$\frac{\partial \theta_i}{\partial \mu_i}=1/\frac{\partial \mu_i}{\partial \theta_i}\\ \frac{\partial \mu_i}{\partial \theta_i}=\frac{b^{\prime\prime}(\theta_i)c^{\prime}(\theta_i)-c^{\prime\prime}(\theta_i)b^{\prime}(\theta_i)}{(b^{\prime}(\theta_i))^2}=b^{\prime}(\theta_i)\text{Var}(Y_i)$$

由 $g(\mu_i)=x_i^T\beta$

$$\frac{\partial \mu_i}{\partial \beta_j}=\frac{\partial \mu_i}{\partial g(\mu_i)}\frac{\partial g(\mu_i)}{\partial \beta_j}=\frac{\partial \mu_i}{\partial g(\mu_i)}x_{ij}$$

因此

$$U_j=\sum ^N_{i=1} \frac{y_i-\mu_i}{Var(Y_i)}x_{ij}\frac{\partial \mu_i}{\partial g(\mu_i)}$$

记黑塞矩阵 $J=\nabla^2l$，一般我们都取它的期望值 $\text{E}(J)$，这里不直接计算 $J$，我们使用费舍尔信息矩阵（Fiesh Infomation Matric），它是一阶梯度协方差矩阵的期望，可以证明它是黑塞矩阵期望的负值，见这里。

$$\begin{aligned} -J_{jk} &= \text{E}(U_jU_k)\\ &=E(\sum ^N_{i=1} \frac{y_i-\mu_i}{Var(Y_i)}x_{ij}\frac{\partial \mu_i}{\partial g(\mu_i)} \cdot \sum ^N_{l=1} \frac{y_l-\mu_l}{Var(Y_l)}x_{lk}\frac{\partial \mu_l}{\partial g(\mu_l)})\\ \end{aligned}$$

由 $Y_i$ 相互独立，$\text{E}((Y_i-\mu_i)(Y_l-\mu_l))=0$，$i \not= l$

$$\begin{aligned} -J_{jk}&=\sum^{N}_{i=1}\frac{\text{E}((Y_i-\mu_i)^2)x_{ij}x_{ik}}{(\text{Var}(Y_i))^2}(\frac{\partial \mu_i}{\partial g(\mu_i)})^2\\ &=\sum^{N}_{i=1}\frac{\text{Var}(Y_i)x_{ij}x_{ik}}{(\text{Var}(Y_i))^2}(\frac{\partial \mu_i}{\partial g(\mu_i)})^2\\ &=\sum^{N}_{i=1}\frac{x_{ij}x_{ik}}{\text{Var}(Y_i)}(\frac{\partial \mu_i}{\partial g(\mu_i)})^2 \end{aligned}$$

因此

$$b_{k+1}=b_k+(\text{E}(J))^{-1}U$$

🔍模型检验

模型检验一般考虑对数似然（比）统计量（Log Likelihood (Ratio) Statistic）。用 $D$，即 Deviance 表示。

$$D=2(l(b_{max};y)-l(b;y))$$

$l$ 是对数似然函数。$b_{max}$ 是全模型的估计的参数，全模型的参数数量在各个模型中是最多的。$b$ 是你所感兴趣的模型的参数估计。$D$ 服从非中心的卡方分布，

$$D\sim \Chi(m-p,v)$$

$m$、$p$ 分别是全模型、所感兴趣的模型的参数数量，$v=2(l(b_{max};y)-l(b;y))$ 如果所感兴趣的模型拟合得全模型差不多好，$v$ 接近于 0。

对于相同连接函数和分布的两个广义线性模型，

$$H_0:\beta=\beta_0=(\beta_1,\cdots,\beta_q)\\ H_1:\beta=\beta_1=(\beta_1,\cdots,\beta_p)\\ q<p$$

考虑统计量

$$\Delta D=D_0-D_1=2(l(b_1;y)-l(b_0;y))$$

如果两个模型拟合效果相近，有 $\Delta D\sim \Chi(p-q)$，当 $\Delta D$ 大于 $\Chi(p-q)$ 的 $\alpha$，拒绝零假设。

?结语

这篇博客稍微简单地回顾了一下广义线性模型的计算方法和模型验证。