🦌鹿心雨的小窝🦌
🦌鹿心雨的小窝
coverPiccoverPic

【算法学习笔记 有序表 3】用 Rust 实现一个替罪羊树

有序表替罪羊树rust算法与数据结构

🎈前言

继续是算法的学习笔记，这篇博客来用 rust 实现一个替罪羊树。

替罪羊树（Scapegoat Tree）是一种自平衡二叉搜索树，由Arne Andersson提出。它通过暴力重构操作来维持平衡，而不是像其他平衡树那样依赖旋转操作。

替罪羊树它有一个初始化时设置的平衡因子属性alpha，取值 (0.5,1)(0.5, 1)。对于一个子树node，节点数量不妨记为node.unique（如果节点统计词频的话，这里的节点是和词频无关的、非重复的节点），当它节点数量满足

α×node.unique>max⁡(node.left.unique,node.right.unique)\alpha\times node.unique>\max(node.left.unique, node.right.unique)

的时候，这个子树会被重构为一棵平衡的二叉搜索树。具体来说，此时我们会对node进行中序遍历，然后再以中序遍历的中点为根，重构一棵平衡的二叉搜索树。

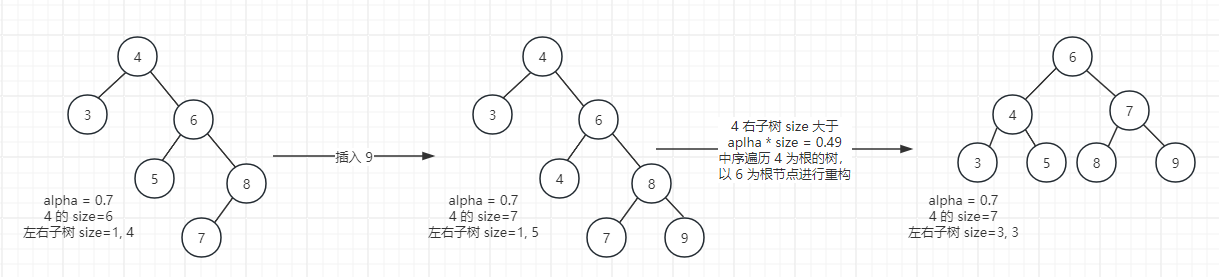
不太严谨地说，重构得越多，树越平衡，但是插入、删除消耗的成本会增加，因为每次重构需要 nO(log⁡n)nO(\log n) 时间复杂度，nn 是重构节点数量。虽然重构消耗大，但是通过设置合理的平衡因子，减少重构次数，它能实现平均 O(log⁡N)O(\log N) 时间复杂度的插入、删除操作，经验上一般这个数值取 0.7。

在删除节点阶段，替罪羊树可以把删除节点的词频置为 0，不必要去每次都调整树结构，从而节省时间。由于有重构的存在，我们只需要在重构时把词频为 0 的节点忽略即可维护树的平衡。

🎆类型定义

没什么好说的，除了平衡二叉树节点常见的key、size、count等属性外，这里需要unique`统计非重复节点个数。此外，在替罪羊树节点上，需要记录重构时的中序遍历、根节点、其亲代节点、以及重构的根节点是左右哪个子树，用来与重构前原有亲代连接。

rust
  1. #[derive(Debug)]
  2. struct ScapegoatTreeNode {
  3.     key: i32,
  4.     count: i32,
  5.     left: OptionScapegoatTreeRc,
  6.     right: OptionScapegoatTreeRc,
  7.     unique: i32,
  8.     size: i32
  9. }
  11. type ScapegoatTreeRc = Rc<RefCell<ScapegoatTreeNode>>;
  12. type OptionScapegoatTreeRc = Option<
  13.     ScapegoatTreeRc
  14. >;
  16. impl ScapegoatTreeNode {
  17.     fn new(key: i32) -> Rc<RefCell<Self>> {
  18.         Rc::new(RefCell::new(Self {
  19.             key,
  20.             count: 1,
  21.             left: None,
  22.             right: None,
  23.             unique: 1,
  24.             size: 1
  25.         }))
  26.     }
  27. }
  29. const LEFT_SIDE: i32 = 1;
  30. const RIGHT_SIDE: i32 = 2;
  32. struct ScapegoatTree {
  33.     root: OptionScapegoatTreeRc,
  34.     alpha: f64,
  35.     collect: Vec<ScapegoatTreeRc>,
  36.     unbalanced_root: OptionScapegoatTreeRc,
  37.     unbalanced_root_parent: OptionScapegoatTreeRc,
  38.     unbalanced_root_side: i32,
  39. }
  41. impl ScapegoatTree {
  42.     fn new(alpha: f64) -> Self {
  43.         ScapegoatTree {
  44.             root: None,
  45.             alpha,
  46.             collect: vec![],
  47.             unbalanced_root: None,
  48.             unbalanced_root_parent: None,
  49.             unbalanced_root_side: 0
  50.         }
  51.     }
  52. }

🎇更新节点

更新操作只需要更新size和unique。

rust
  1. fn size(node: OptionScapegoatTreeRc) -> i32 {
  2.     match node {
  3.         None => 0,
  4.         Some(x) => {
  5.             x.borrow().size
  6.         }
  7.     }
  8. }
  9. fn unique(node: OptionScapegoatTreeRc) -> i32 {
  10.     match node {
  11.         None => 0,
  12.         Some(x) => {
  13.             x.borrow().unique
  14.         }
  15.     }
  16. }
  17. fn update(node: OptionScapegoatTreeRc) {
  18.     match node {
  19.         None => {},
  20.         Some(x) => {
  21.             let left = x.borrow().left.clone();
  22.             let right = x.borrow().right.clone();
  23.             let count = x.borrow().count;
  24.             x.borrow_mut().size = Self::size(left.clone()) + Self::size(right.clone()) + count;
  25.             x.borrow_mut().unique = Self::unique(left.clone()) + Self::unique(right.clone()) + if count > 0 {
  26.                 1
  27.             } else {
  28.                 0
  29.             }
  30.         }
  31.     }
  32. }

⚖判断平衡性

我们来用一个工具方法判断树节点的平衡性，在下面增加删除节点时会用到。

rust
  1. fn balance(&self, node: OptionScapegoatTreeRc) -> bool {
  2.     match node {
  3.         None => return true,
  4.         Some(x) => {
  5.             return self.alpha * x.borrow().unique as f64 >= i32::max(
  6.                 Self::unique(x.borrow().left.clone()),
  7.                 Self::unique(x.borrow().right.clone())
  8.             ) as f64;
  9.         }
  10.     }
  11. }

💥重构平衡树

当增加、删除操作破坏了树的平衡性时，替罪羊树将会指定待重构的根节点，和它的亲代节点以及它是哪个子树（下面再说）。然后替罪羊树开始重构平衡树，中序遍历待重构的根节点收集count非 0 的节点，然后从中点开始前序地重新组织平衡树。

rust
  1. fn inorder(&mut self, node: OptionScapegoatTreeRc) {
  2.     match node {
  3.         None => {},
  4.         Some(x) => {
  5.             self.inorder(x.borrow().left.clone());
  6.             if x.borrow().count > 0 {
  7.                 self.collect.push(x.clone());
  8.             }
  9.             self.inorder(x.borrow().right.clone());
  10.         }
  11.     }
  12. }
  13. fn build(&mut self, l: i32, r: i32) -> OptionScapegoatTreeRc {
  14.     if l > r {
  15.         return None
  16.     }
  17.     let mid = (l + r) / 2;
  18.     let head = self.collect[mid as usize].clone();
  19.     head.borrow_mut().left = self.build(l, mid - 1);
  20.     head.borrow_mut().right = self.build(mid + 1, r);
  21.     Self::update(Some(head.clone()));
  22.     Some(head)
  23. }
  24. fn rebuild(&mut self) {
  25.     match self.unbalanced_root.clone() {
  26.         None => {},
  27.         Some(x) => {
  28.             self.collect.clear();
  29.             self.inorder(Some(x.clone()));
  30.             if self.collect.len() > 0 {
  31.                 if self.unbalanced_root_parent.is_none() {
  32.                     self.root = self.build(0, self.collect.len() as i32 - 1);
  33.                 } else if self.unbalanced_root_side == LEFT_SIDE {
  34.                     self.unbalanced_root_parent.clone().unwrap().borrow_mut().left = self.build(0, self.collect.len() as i32 - 1);
  35.                 } else {
  36.                     self.unbalanced_root_parent.clone().unwrap().borrow_mut().right = self.build(0, self.collect.len() as i32 - 1);
  37.                 }
  38.             }
  39.         } 
  40.     }
  41. }

➕增加节点

在增加删除节点时，我们需要指定待重构根节点的信息。这里会可能存在一种情况，如果子树及其后代某个子树都是不平衡的，此时需要重构的只有最高层的子树，因为它会把后代不平衡的子树也重新排序。因此我们采用后序遍历，这时指定的待重构节点也是最高层的节点。.

rust
  1. fn insert(&mut self, key: i32) {
  2.     self.unbalanced_root = None;
  3.     self.unbalanced_root_parent = None;
  4.     self.unbalanced_root_side = 0;
  5.     self.insert_helper(self.root.clone(), self.unbalanced_root_parent.clone(), self.unbalanced_root_side, key);
  6.     self.rebuild();
  7. }
  8. fn insert_helper(&mut self, node: OptionScapegoatTreeRc, parent: OptionScapegoatTreeRc, side: i32, key: i32) {
  9.     match node {
  10.         None => {
  11.             if parent.is_none() {
  12.                 self.root = Some(ScapegoatTreeNode::new(key));
  13.             } else if side == LEFT_SIDE {
  14.                 parent.clone().unwrap().borrow_mut();
  15.                 parent.clone().unwrap().borrow_mut().left = Some(ScapegoatTreeNode::new(key));
  16.             } else {
  17.                 parent.clone().unwrap().borrow_mut().right = Some(ScapegoatTreeNode::new(key));
  18.             }
  19.         },
  20.         Some(x) => {
  21.             if x.borrow().key == key {
  22.                 x.borrow_mut().count += 1;
  23.             } else if x.clone().borrow().key > key {
  24.                 let left = x.borrow().left.clone();
  25.                 self.insert_helper(left, Some(x.clone()), LEFT_SIDE, key);
  26.             } else {
  27.                 let right = x.borrow().right.clone();
  28.                 self.insert_helper(right, Some(x.clone()), RIGHT_SIDE, key);
  29.             }
  30.             Self::update(Some(x.clone()));
  31.             if !self.balance(Some(x.clone())) {
  32.                 self.unbalanced_root = Some(x.clone());
  33.                 self.unbalanced_root_parent = parent.clone();
  34.                 self.unbalanced_root_side = side;
  35.             }
  36.         }
  37.     }
  38. }

❌删除节点

类似地，后序遍历找到待删除节点，把count减 1，由于有重构的存在，并不需要每次删除时调整子树结构。另外，这里借助查询节点排序的rank方法（下面说到）来确定节点是否存在。

rust
  1. fn remove(&mut self, key: i32) -> bool {
  2.     if self.rank(key) != self.rank(key + 1) {
  3.         self.unbalanced_root = None;
  4.         self.unbalanced_root_parent = None;
  5.         self.unbalanced_root_side = 0;
  6.         self.remove_helper(self.root.clone(), self.unbalanced_root_parent.clone(), self.unbalanced_root_side, key);
  7.         self.rebuild();
  8.         true
  9.     } else {
  10.         false
  11.     }
  12. }
  13. fn remove_helper(&mut self, node: OptionScapegoatTreeRc, parent: OptionScapegoatTreeRc, side: i32, key: i32) {
  14.     match node {
  15.         None => {},
  16.         Some(x) => {
  17.             if x.borrow().key == key {
  18.                 x.borrow_mut().count -= 1;
  19.             } else if x.borrow().key < key {
  20.                 let right = x.borrow().right.clone();
  21.                 self.remove_helper(right, Some(x.clone()), RIGHT_SIDE, key);
  22.             } else {
  23.                 let left = x.borrow().left.clone();
  24.                 self.remove_helper(left, Some(x.clone()), LEFT_SIDE, key);
  25.             }
  26.             Self::update(Some(x.clone()));
  27.             if !self.balance(Some(x.clone())) {
  28.                 self.unbalanced_root = Some(x.clone());
  29.                 self.unbalanced_root_parent = parent.clone();
  30.                 self.unbalanced_root_side = side;
  31.             }
  32.         }
  33.     }
  34. }

🔟排序的查询

查询某个key在有序表中的顺序，以及查询有序表中排第idx位的节点，和之前写的 AVL 平衡树的操作类似。

rust
  1. fn rank(&self, key: i32) -> i32 {
  2.     Self::rank_helper(self.root.clone(), key) + 1
  3. }
  4. fn rank_helper(node: OptionScapegoatTreeRc, key: i32) -> i32 {
  5.     match node {
  6.         Some(cur) => {
  7.             if cur.borrow().key >= key {
  8.                 let left = cur.borrow().left.clone();
  9.                 Self::rank_helper(left, key)
  10.             } else {
  11.                 let left = cur.borrow().left.clone();
  12.                 let right = cur.borrow().right.clone();
  13.                 Self::size(left) + cur.borrow().count + Self::rank_helper(right, key)
  14.             }
  15.         },
  16.         None => 0
  17.     }
  18. }
  19. fn index(&self, idx: i32) -> i32 {
  20.     Self::index_helper(self.root.clone(), idx)
  21. }
  22. fn index_helper(node: OptionScapegoatTreeRc, idx: i32) -> i32 {
  23.     match node {
  24.         None => i32::MIN,
  25.         Some(x) => {
  26.             let left = x.borrow().left.clone();
  27.             let left_size = Self::size(left.clone());
  28.             let current_count = x.borrow().count;
  29.             if left_size >= idx {
  30.                 let ans = Self::index_helper(left, idx);
  31.                 return ans
  32.             } else if left_size + current_count >= idx {
  33.                 return x.borrow().key
  34.             } else {
  35.                 let right = x.borrow().right.clone();
  36.                 let ans = Self::index_helper(right, idx - left_size - current_count);
  37.                 return if ans != i32::MIN { ans } else { i32::MAX }
  38.             }
  39.         }
  40.     }
  41. }

🖇前驱后继的查询

这也就是找到小于节点的最大值和大于节点的最小值。因为有count为 0 的节点，方便起见，借助rank和index方法来完成查询。

rust
  1. fn pre(&self, key: i32) -> i32 {
  2.     let rank = self.rank(key);
  3.     if rank == 1 {
  4.         i32::MIN
  5.     } else {
  6.         self.index(rank - 1)
  7.     }
  8. }
  9. fn next(&self, key: i32) -> i32 {
  10.     let rank = self.rank(key + 1);
  11.     if rank == Self::size(self.root.clone()) + 1 {
  12.         i32::MAX
  13.     } else {
  14.         self.index(rank)
  15.     }
  16. }

🎁结语

这是复习数据结构的第三篇博客，用 rust 实现了一个替罪羊树。

参考：
【算法讲解150【扩展】有序表专题3-替罪羊树】 https://www.bilibili.com/video/BV1GqDSYbEPR/?share_source=copy_web&vd_source=a06db201a5f7fab5fe54f12bff164f84

上一篇：【算法学习笔记 有序表 2】用 Rust 实现一个跳表
下一篇：浏览器事件循环宏任务还有优先级？
0 条评论未登录用户
Ctrl or + Enter 评论
© 2023-2025 LittleRangiferTarandus, All rights reserved.
🌸 Run